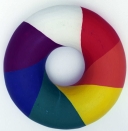
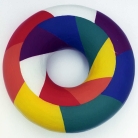
Ungar-Leech Seven Coloration of the Torus
by
Norton Starr
The above figures show the two sides of a torus on which is drawn a map of seven countries, each contacting all the other six. [Click on either image for larger view.] This demonstrates that Heawood’s theorem, which asserts that any map on the torus can be properly colored with at most seven colors, is best possible. (Reasonable restrictions, such as the requirement that each country be connected (no separated portions like Alaska) are presumed.) The original map of seven countries arranged so as to force the use of seven colors, was worked out by Percy J. Heawood. Its symmetric portrayal shown here was independently developed by Peter Ungar and John Leech. I made the displayed model out of hydrostone in 1972. Its outer diameter is 9 inches, and it consists of two toroidal halves glued together. Each half was cast in a wood mold prepared for me by the machine shop of the Department of Physics.
References and Remarks
Anatol Beck, Michael N. Bleicher, and Donald W. Crowe show how one might envision the construction and coloring of such a torus in Excursions into Mathematics, Worth Pub., 1969. (See the color figures on the frontispiece, facing the title page, and the (equivalent) monochrome images on p. 67.) This book has been updated and reissued as Excursions into Mathematics: The Millennium Edition (paperback) by A K Peters, Ltd., 2000. (See p. 64.)
sarah-marie belcastro and Carolyn Yackel designed and engineered the fabrication of a torus displaying seven countries, each contacting the other six. The considerable work involved in this development is described in their informative chapter “The Seven-Colored Torus: mathematically interesting and nontrivial to construct” for the book arising from G4G7, Homage to a Pied Puzzler, Ed Pegg Jr., Alan H. Schoen, and Tom Rodgers, eds., A K Peters, August 2008. Yackel’s crocheted realization of this is illustrated in their chapter. It also appears here, on the right in the picture titled "Doughnut Math."
Other good illustrations, along with some history, are given in the last three pages of H. S. M. Coxeter, The four-color map problem, 1840-1890, The Mathematics Teacher 52 (April, 1959), 283-289.
A guide to drawing the seven regions on a torus is provided on page 168 of Mathematical Models (2nd ed.), H. Martyn Cundy and A. P. Rollett, Oxford University Press, 1961. (Most of my own boundaries were located by running a taut string between pairs of points on the model, a method suggested by Geoffrey A. Wilson, a student in my course Geometry and Finite Mathematics, spring 1972.)
A picture of my plaster torus appears on the front cover of Explorations in Topology: Map Coloring, Surfaces, and Knots, David Gay, Elsevier, 2007.
Susan Goldstine (Amherst College, 1993) displays on her site a variety of seven colorations of maps on unusual tori, along with a template and guidelines for construction. She is also on p. 113 of her chapter Fortunatus’s Purse in Making Mathematics with Needlework, sarah-marie belcastro and Carolyn Yackel, eds., A K Peters, Ltd., 2008.
The first known construction of a map of seven regions on a torus, each contacting each of the other six, was given by Percy J. Heawood, a pioneer in the study of map coloring. See his Map-colour theorem, Quarterly Journal of Pure and Applied Mathematics 24 (1890), 332-338. A more accessible image of this map appears on p. 114 of Graph Theory 1736-1936, N. L. Biggs, E. K. Lloyd, and R. J. Wilson, Oxford Univ. Pr., 1976.
Coxeter (op. cit.) attributes the symmetric representation of seven regions on a torus displayed above to John Leech in 1953. See John Leech, Seven Region Maps on a Torus, The Mathematical Gazette, 39, No. 328 (May, 1955), 102-105.
Leech acknowledges (footnote, p. 103) the essential equivalence of his scheme to that in Peter Ungar, On Diagrams Representing Maps, Journal of the London Mathematical Society, 28 (1953), 336-342. In turn, Ungar acknowledges the then yet unpublished similar dissection of Leech (footnote, p. 342.)