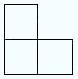To play a physical version of this puzzle, using 21 actual tromino tiles, a single square piece, and an 8×8 checkerboard-like base, first position the single square tile on any one of the 64 square locations on the base. Then fill the remaining 63 squares with the trominoes so that there is no overlap and no unfilled square. Such a solution to the puzzle is called a tiling of the 8×8 square. Alternatively, start by successively placing trominoes into the checkerboard base (each such tile occupying only three squares of the grid pattern), and when all 21 are positioned, place the single square tile in the one position that remains available.

Here's the background to the commercial version of this puzzle, marketed by Kadon Enterprises. At the January, 2000 annual meeting of the Mathematical Association of America, Arthur Benjamin received the Haimo award for distinguished college teaching. In his acceptance speech he sketched his favorite proof by induction. This reasoning assures that a 2ⁿ×2ⁿ celled square (i.e. a generalized checkerboard with 2ⁿ squares along each side) with one cell occupied, can always be tiled by trominoes. Three years after hearing Benjamin's remarks I was giving a lecture on induction and recalled his favorite proof. Supplementing my prepared examples, I ad libbed this classic argument, due to Solomon Golomb. Thinking that an actual puzzle of this sort would add an element of reality and might spark interest in the method of induction, I sent a note to Kadon, a leading puzzle maker, to see if they had one I could purchase. They didn't, so I asked if they would make some to my specifications. A series of emails with Kate Jones, President of Kadon, led to a puzzle of the sort illustrated above left. She suggested using several different colors for the tromino tiles, making this a more interesting puzzle than I had originally envisioned. I opted for cooler, translucent tiles rather than bold, opaque ones, and chose blue, aqua and amethyst for the trominoes.

Kate asked if I would let Kadon add the puzzle to the array of items they sell and I readily agreed - I only wanted some for my own use. To my surprise, she declared that I would be receiving royalties. That was never my goal, and all my royalties are donated to Amherst College and the Mathematical Association of America.

Kadon brought out the puzzle under the name "Vee-21"; see www.gamepuzzles.com/polycub2.htm#V21. This commercial version, in three vivid, translucent acrylic colors, comes with a forty page brochure offering a number of enhancements to the basic puzzle. Kate contributed some extensions of the puzzle, some two-person strategy games, and the suggestion of color separation requirements for tilings one might attempt. She also discovered the aesthetic possibilities in making symmetrical patterns. Kate invited Oriel Maximé to contribute some of his maze-like challenges for tiling with the trominoes, and the brochure includes a variety of rectangular templates with strategically chosen lines of the grids darkened to serve as barriers across which trominoes may not be placed.

Two interactive computer puzzles of this sort are provided on this CD. The 8-by-8 puzzle was developed by two of my students, while a departmental colleague contributed the M-by-N puzzle. The M-by-N puzzle (plays on most systems but may be slow to load) is somewhat more flexible, allowing the choice of any number of rows and columns between 2 and 32, inclusive. The 8-by-8 puzzle (plays best with Internet Explorer on a PC) has a different mouse action and is usefully restricted to three colors of tromino. Directions are given with each. The CD and the Kadon versions both have unusual breadth of appeal, intriguing for four year olds as well as seasoned puzzlers.

The proof that for any positive integer  n,  a 2ⁿ×2ⁿ square with one cell occupied (a "deficient" square) can always be tiled by trominoes is due to Solomon Golomb. He published it in his 1954 article [9] in the American Mathematical Monthly. As noted above, it was to illustrate Golomb's argument for 2ⁿ×2ⁿ deficient squares that the puzzle was commissioned. The same article introduced in print the term tromino and its generalization, polyomino. A polyomino is a connected array of identical squares having the property that any two squares either do not touch or else meet along an entire, common edge. The only two tromino shapes are three squares in a row and the L-shape of this puzzle, and here "tromino" only refers to the latter.

Golomb's proof is a first-rate example of mathematical induction. Beyond the sheer elegance of the argument, it's a rare instance of a nonnumerical application of the method. This stands in contrast to the examples and exercises often found in textbook treatments of induction, which typically consist of a variety of formulas for finite sums, inequalities, and the like. The proof's first appearance in a popular medium was in Joseph Madachy's Recreational Mathematics Magazine (RMM), where Golomb included it in the first of his four-part series of articles on polyominoes published in RMM [10]. In Martin Gardner's seminal May, 1957 Scientific American column introducing polyominoes to the wider public, he remarked that "a board with one square missing at any point, can be covered by 21 right trominoes" [6, p. 154]. For his first book of collected Mathematical Games columns, Gardner elaborated by remarking that "an ingenious induction argument demonstrates that 21 right trominoes and one monomino will cover the 8-by-8 board regardless of where the monomino is placed" [8, p. 126].

The tromino tiling argument for deficient checkerboards and the general 2ⁿ×2ⁿ theorem has appeared in a succession of books since the Monthly and RMM articles. It was explained in Golomb's classic Polyominoes [11, 1965, pp. 21-22] and in the second edition of that book [11, 1994, p. 5]. The second edition gives a rich history and an extensive survey of this intriguing subject, and is filled with pictures and puzzles. Its 22 pages of references, citing both books and articles, are an added bonus. The index of names lists 81 individuals, quite a few referred to more than once in the body of the book. Many of these will be recognized by game aficionados and amateur mathematicians as well as by professionals in either area. A description of the book is given in the review [17] by George Martin. In 1976, Ross Honsberger gave a lucid, detailed application of Golomb's argument to the checker board in his Mathematical Gems II [13, p. 61]. The basic idea of the proof is also mentioned in George E. Martin's book devoted to polyomino tilings [16, pp. 27-28]. David Singmaster's review [21] of this latter book is particularly interesting, for it gives a beautiful sketch of the subject and its history.

This topic also is increasingly common fare for texts and problem books. For instance, it appears in the discrete mathematics texts of Susanna Epp [5, p. 234], Richard Johnsonbaugh (who mentions tromino tilings of rectangles as arising in VLSI layout design) [14, pp. 58-59], and Kenneth Rosen [20, pp. 247-8]. Tromino tiling is also treated in Daniel Velleman's book about constructing proofs [22, pp. 271-275] and the problem books by John P. D'Angelo & Douglas B. West [1, p. 75] and by Jiří Herman, Radan Kučera & Jaromír Šimša [12, p. 271]. The most crystalline illustration of the Golomb argument is Roger Nelsen's spare "proof without words," given in his second book of that title [19, p. 123].

This area of recreational mathematics has benefited from a continuing stream of investigation and suggested problems. In 1985 and 1986, I-Ping Chu and Richard Johnsonbaugh studied the question of tiling deficient n×n boards, where  n  no longer need be a power of 2, and, more generally, deficient and non-deficient rectangular boards [3, 4]. George Martin's book included a whole chapter devoted to tromino tilings [16, pp. 23-37]. Coloration problems for tromino tiling are treated by Ilvars Mizniks, who acknowledges the Kadon Vee-21 color selection page as inspiration for his research [18]. The 2004 article [2] by J. Marshall Ash and Solomon Golomb, about tromino tiling of deficient rectangles, contains several new and basic results, one of which answers an old question of Chu and Johnsonbaugh. Ash and Golomb end with an open problem about 2-deficient rectangles (rectangles with two cells removed).

The Internet is a good source of tiling displays and information. For instance, a search on "tromino" and "tiling" turns up applets such as those by Alexander Bogomolny at www.cut-the-knot.org/Curriculum/Games/TrominoPuzzle.shtml and Christopher Mawata at www.utc.edu/Faculty/Christopher-Mawata/trominos/, which illustrate tromino puzzles of several sizes.

Another direction is three dimensional. Consider a cube of side length 2ⁿ, containing 2³ⁿ unit cells, one of which is occupied (single deficiency.) Can the remaining cells be tiled with three dimensional trominoes (three cubes in an L-shape, with two of them meeting the third on two adjacent faces of the latter)? The necessary condition that 2ⁿ = 3k + 1 turns out to be sufficient as well. [Submitted.] The case of a 4×4×4 cube presents some modest challenges that may amuse young puzzlers.

Simpler problems readily suggest themselves and have been considered by numerous others. For instance, can the full 3×3 and 6×6 square arrays be tiled with trominoes? Can every deficient 5×5 and 7×7 square array be tiled? These latter two puzzles are more challenging than the full 3×3, 6×6, and deficient 8×8 cases. Going further, readers may consider tilings of various rectangular arrays - see the references below. When using a version with more than one color of tromino, such as the Kadon Vee-21, consider various color constraints. For instance, try arranging the tiles so that no two of the same color share an edge. In the opposite direction, try to group as many tiles of one color together as possible. For both these pattern types, try further to make the tiling appear symmetric about a diagonal or about a horizontal or vertical line. The opportunities for fun and discovery are numerous. Different size rectangles can be studied by clicking on the M-by-N puzzle. For color pattern experiments, the Kadon puzzle is best.